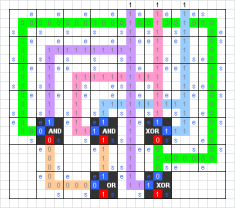
Solución a un 3D Squares

Hay puzzles que les regalan a los niños que parecen triviales y no lo son, a veces ni para los niños ni para los adultos. Para mi este es un caso claro.
Para resolverlo tuve que programar un solucionador en TOL que no resulto muy complicado. De hecho mucho menos complicado que resolver manualmente el puzzle 3D Squares. Aunque el código completo junto con su traza de ejecución puede obtenerse en PDF al final de este post, pongo a continuación en algoritmo recursivo fundamental. Este algoritmo encuentra 4 soluciones iguales, pues unas resultan de un giro de 90º de otras:
///////////////////////////////////////////////////////////////////
Real SolCua(Set entSol, Set entPie) // Resuelve
///////////////////////////////////////////////////////////////////
{
Real crdSol = Card(entSol);
Text Write(FormatReal(crdSol,"%.0lf"));
If(EQ(crdSol, 9), SolVer(entSol), // Ha encontrado una solucion
{ // Busca soluciones
EvalWhile(entPie, Real(Text unoPie)
{
Set salPie = entPie - [[unoPie]];
Set varPie = VarAll(unoPie);
EvalWhile(varPie, Real(Text unoVar)
{
Set salSol = entSol << [[ unoVar ]];
If(SolBue(salSol), SolCua(salSol, salPie), FALSE)
})
})
})
};
Programación de la solución del 3D Squares y traza de ejecución
Ver el problema y las 4 soluciones del 3D Squares